1. Web 中的矩阵
在 Web 开发中经常见到矩阵的身影,比如:
-
SVGGraphicsElement.getScreenCTM() 返回的 DOMMatrix 是一个
4 X 4的矩阵,适用于 2D 和 3D 操作,包括旋转和平移。 -
CSS 函数
matrix(a, b, c, d, tx, ty)指定了一个由 6 个值组成的 2D 变换矩阵。齐次坐标下的表示为:$\begin{bmatrix} a & c & t_x \\ b & d & t_y \\ 0 & 0 & 1 \end{bmatrix}$
为了搞清楚其含义,特意去学习了下 GAMES101-现代计算机图形学入门-闫令琪 课程的前几节课,里面详细地讲了向量和矩阵的相关知识。
2. 向量乘法
2.1 向量点乘
-
几何定义:
$\vec a \cdot \vec b = |\vec a||\vec b|cos \theta$
其中 $|\vec a|$ 和 $|\vec b|$ 分别表示 $\vec a$ 和 $\vec b$ 的模长,$\theta$ 表示两个向量之间的角度。
$cos \theta = \hat a \cdot \hat b$
其中 $\hat a$ 和 $\hat b$ 均为单位向量。
-
代数定义:
$\vec a \cdot \vec b = \vec a^T \vec b = \begin{pmatrix} x_a & y_a & z_a \end{pmatrix} \begin{pmatrix} x_b \\ y_b \\ z_b \end{pmatrix} = x_ax_b + y_ay_b + z_az_b$
实际用途:
- 计算两个向量之间的夹角余弦。
- 计算一个向量到另一个向量的投影。
- 判断一个向量在另一个向量的前面或后面。
2.2 向量叉乘
-
几何定义:
$\vec a \times \vec b = ||a||||b||sin (\theta)n$
其中 $\theta$ 表示 a 和 b 在它们所定义的平面上的夹角,$||a||$ 和 $||b||$ 是向量的模长,n 为 a、b 所构成的平面的垂直单位向量,方向由右手定则决定。
-
代数定义:
$\vec a \times \vec b = A^* b = \underbrace {\begin{pmatrix} 0 & -z_a & y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0 \end{pmatrix}}_{dual \ matrix \ of \ vector \ a} \begin{pmatrix} x_b \\ y_b \\ z_b \end{pmatrix} = \begin{pmatrix} y_az_b - y_bz_a \\ z_ax_b - x_az_b \\ x_ay_b - y_ax_b \end{pmatrix}$
实际用途:
- 判断左右。
- 判断内外。
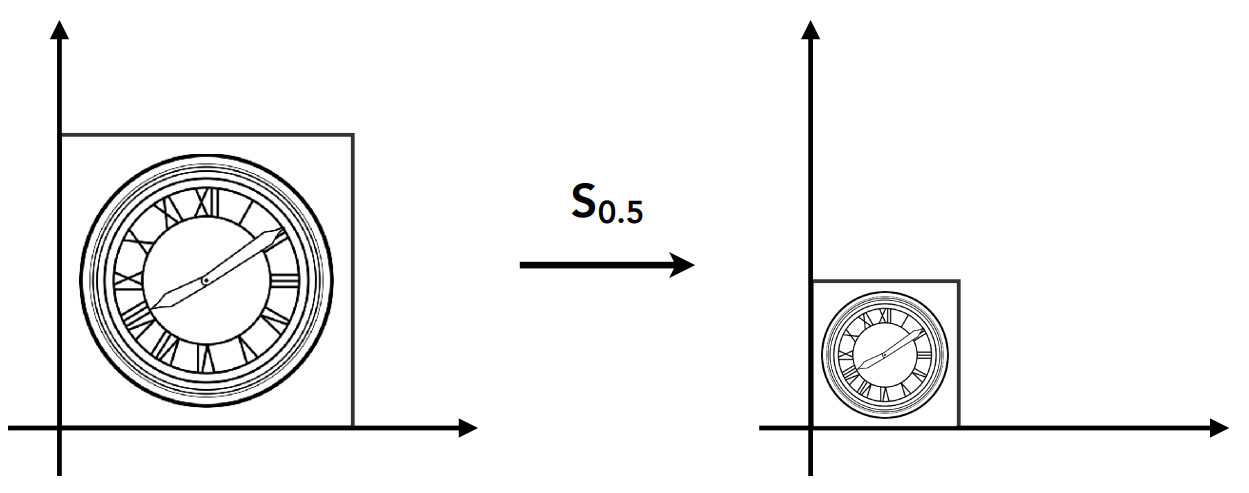
3.缩放矩阵
等比缩小 0.5,下图中的 s = 0.5 :
用矩阵表示:
$\begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix} = \begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin {bmatrix} 0.5x \\ 0.5y \end{bmatrix}$
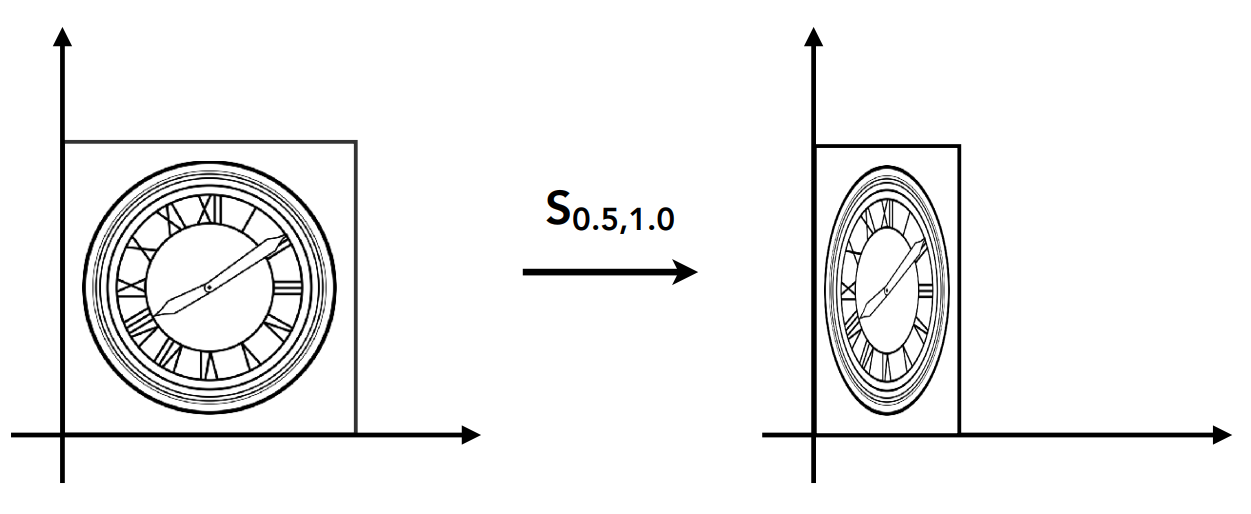
非等比缩放:
用矩阵表示:
$\begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix} = \begin{bmatrix} 0.5 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0.5x \\ y \end{bmatrix}$
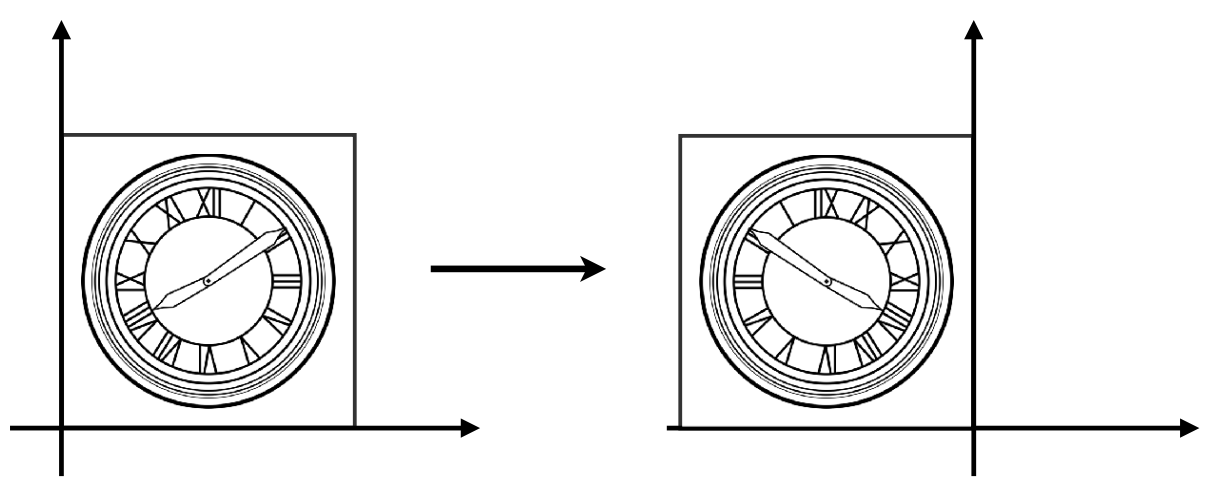
4.对称矩阵
沿 y 轴对称:
用矩阵表示:
$\begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} -x \\ y \end{bmatrix}$
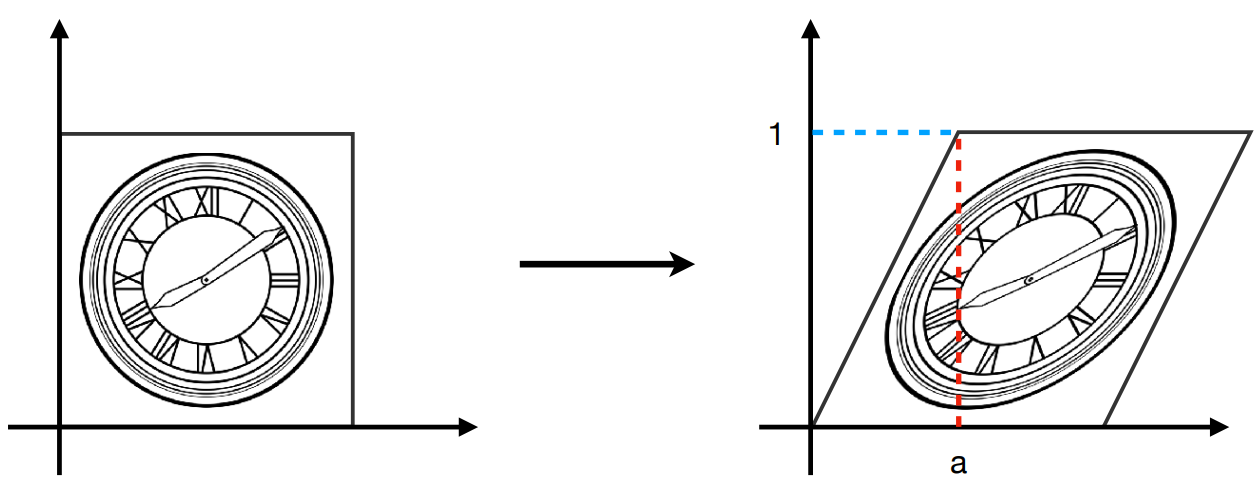
5.切变矩阵
沿 x 轴切边:
提示:
- 在
y = 0处的水平移动是0。 - 在
y = 1处的水平移动是a。 - 垂直移动始终为
0。
因此变化后的 x/y 坐标满足:
$x^{\prime} = x + ay$
$y^{\prime} = y$
用矩阵表示:
$\begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix} = \begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x + ay \\ y \end{bmatrix}$
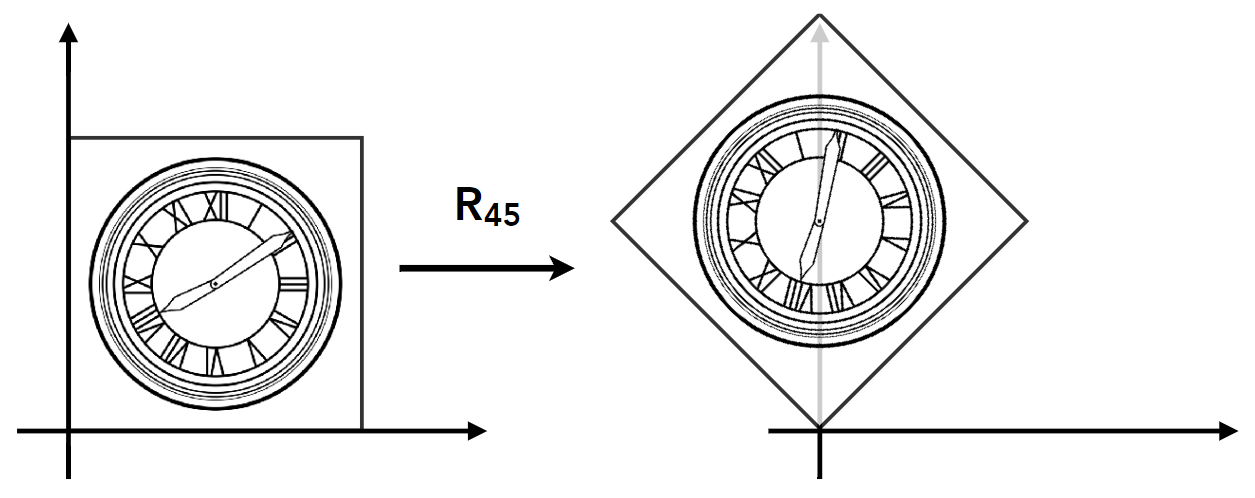
6.旋转矩阵
逆时针旋转 $45^{\circ}$ :
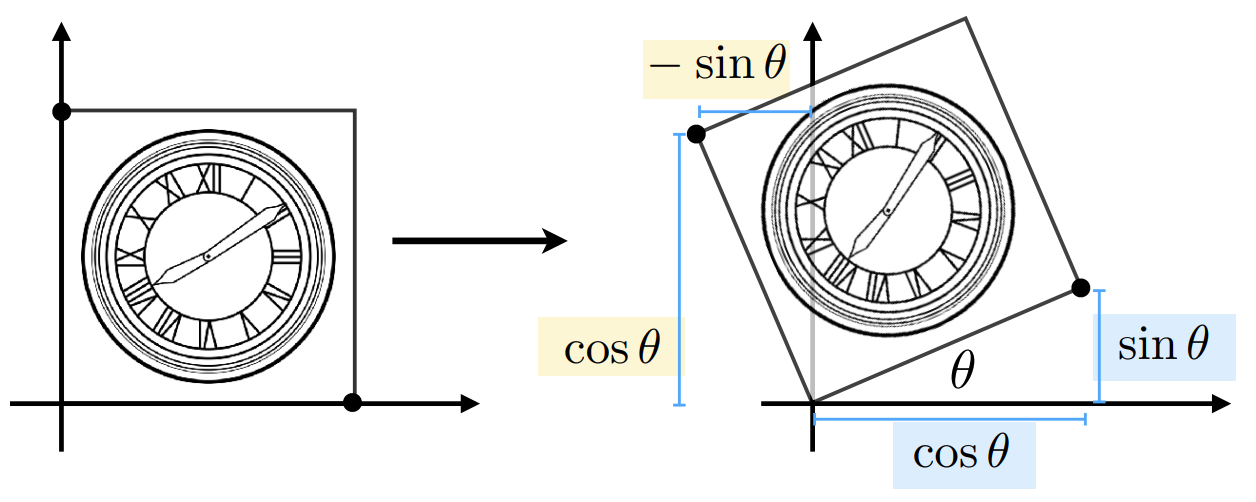
推导过程:
坐标变化:
-
左上角 $[0, \ 1]$ 变为 $[-sin\theta, \ cos\theta]$
$\begin{bmatrix} a & c \\ b & d \end{bmatrix}\begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} -sin\theta \\ cos\theta \end{bmatrix}$
由 $a\cdot0 + c\cdot1 = -sin\theta$ 得出 $c=-sin\theta$ 。
由 $b\cdot0 + d\cdot1 = cos\theta$ 得出 $d=cos\theta$ 。
-
右下角 $[1, \ 0]$ 变为 $[cos\theta, \ sin\theta]$
$\begin{bmatrix} a & c \\ b & d \end{bmatrix}\begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} cos\theta \\ sin\theta \end{bmatrix}$
由 $a\cdot1 + c\cdot0 = cos\theta$ 得出 $a=cos\theta$ 。
由 $b\cdot1 + d\cdot0 = sin\theta$ 得出 $b=sin\theta$ 。
因此逆时针旋转一个角度 $\theta$ 的变换矩阵为 :
$\begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix} = \begin{bmatrix} cos \theta & -sin \theta \\ sin \theta & cos \theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}$
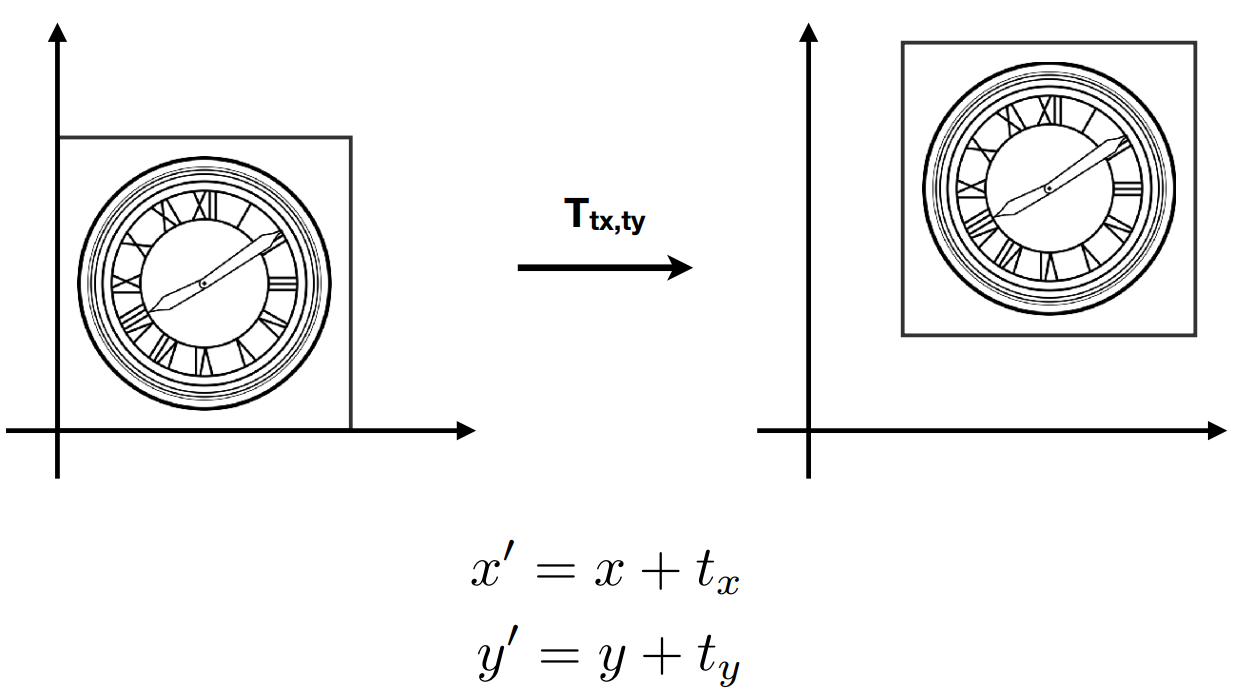
7.平移矩阵
x方向平移 tx ,y方向平移 ty :
用矩阵表示为 :
$\begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix}$
上述变化并不是线性变换,因此我们引入齐次坐标这个概念去解决平移的问题:
增加第三个坐标(w坐标)
2D 点: $(x, \ y, \ 1)^T$
2D 向量: $(x, \ y, \ 0)^T$
$\begin{bmatrix} x^{\prime} \\ y^{\prime} \\ w^{\prime} \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} x + t_x \\ y + t_y \\ 1 \end{bmatrix}$
8.使用齐次坐标的2D变换
-
缩放:
$S(s_x, s_y) = \begin{pmatrix} s_x & 0 & 0 \\ 0 & x_y & 0 \\ 0 & 0 & 1 \end{pmatrix}$
-
旋转:
$R(\alpha) = \begin{pmatrix} cos\alpha & -sin\alpha & 0 \\ sin\alpha & cos\alpha & 0 \\ 0 & 0 & 1 \end{pmatrix}$
-
移动:
$S(s_x, s_y) = \begin{pmatrix} 1 & 0 &t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix}$